CARDBOARD BOXES!
 We bought some speakers,
We bought some speakers,my little bro drew my face,
I struggled to breathe,
It was awesome.
Measure For Measure
So call back auditions were last night. And WOW, what a fantastic cast we have. The auditions were so much fun as well. Mostly a bunch of theatre sports and some individual monologues. It was a little bit nerves, a little bit because I was surrounded by hilarious people but I was in hysterics most of the night. 10/10 would audition again! I'm so excited to start rehearsals with whatever part I get, even if I only have one line. That is how awesome the cast is! <3
Difficulty Ratings
So I've decided that I'm going to introduce difficulty ratings to different sections in my blog. Though I encourage you to give the harder things a read this means that you can just cruise through the easier parts if you want :DThis is the system I will be using:
5 - ((I Don't Even)): This means it's beyond me and my understanding. There probably won't be much of this because if I don't understand something I will probably not write it so that you all still think I'm smart.
4 - ((Break a Sweat)): This means that I found it difficult but got there in the end
3 - ((So-So): It was relatively easy for me as a person with 3 years of mechanical engineering under my belt to understand when broken down into steps
2 - ((All Good)): Relatively easy for me to understand
1 - ((Easy as Pie)): Easy as Pie!
So this is all based around my experience and there are probably geniuses who will find all of it easy and there will also be others who don't have a big background in math or science who might find it harder. If you spend the time thinking about it critically though, you will come to understand it which is the really cool thing about math and physics!!
Exponential Functions ((2))
So here's a nifty trick, if you're ever out and about and have forgotten your phone or calculator and really really really need to know what the exponential function of some number is (e^x) all you have to do is use the algorithm
x = some number for examble 2!
e
= the exponential function
k
= a number which starts at zero and increases in jumps of 1 each additional
term
!
= means factorial. When a number has a factorial sign beside it you write down
all the whole numbers from 1 to your number and put multiplication signs in
between i.e. 4! = 1x2x3x4 = 24!!
So the equation says to begin with k = 1 and go to k = infinity but you don't need to do that. Noone does that because that's a really lame thing to do with you life and you're always going to fail. You just need to go until the equation converges. And by converging I mean when you are adding extra terms to the equation and it doesn't seem to be making much difference. Give it a go with x = 1.
See if you can "converge" to 2.7 :D go on !
Here's just one example of where it might come in handy...
Matrix Exponential Function ((3))
So if you want to give this a go but you're unclear about matrices I explain them here.You also might want to know more about matrix operations (multiplication, dot products, determinants etc) you can find them here because it will take SOOO much time to explain them all.
So we are basically just going to take the above equation for a linear equation and magic it to make it work for a matrix as well. The other thing we're going to do is add variation with time by putting in the scalar value t because that will make our equation really useful. A lot of applied math varies with time!
So we want to work out e^(At) which is the exponential function of a matrix which varies with time. Here's the equation we have to use. See if you can spot the similarities to the equation above...
So when we are expanding this out, instead using a 1 for the first term as we did in the above linear case we now use the Identity matrix [1,0 ; 0,1] for when k = 0 and . We simply expand as above to get our answer using a similar method as above. Let's do an example!!
In this example A = [0,1;1,0]; We want to find e^At
using the equation above our terms are (just expanding out the equation):
= I + tA + (t^2)(A^2)/2 + (t^3)(A^3)/(2x3) + (t^4)(A^4)/(2x3x4) ...
Subbing A into our matrix and using matrix formatting we get
Which seems really messy until we do this magical magical thing involving the series definition on this page. Now our matrix simplifies really beautifully to this...
Incidentally this is actually how your calculator calculates the sin and cos function. Think about it, it would be completely unreasonable to have manually tried to program in the sin and cos function. The calculator must be working it out somehow and this is exactly how!
Modal Method - (the easy way)
So here's a wonderful application for the diagonalisation stuff we learnt about in one of my previous blogs! I love it when stuff is useful :D
We can calculate e^At in an easier way than the one above IF we know that matrix A is diagonalisable.
BUT I'm going to save that for another night because my bed is calling and I still have a speech to write.
GOODNIGHT EVERYONE!
<a href="http://www.bloglovin.com/blog/12644549/?claim=ar6ycwtrq4v">Follow my blog with Bloglovin</a>

.JPG)


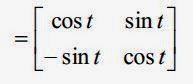
No comments:
Post a Comment