Mages in Space! (who do their hair nicely)
So its pretty clear for those of you who have spent enough time with me, that I adore being a girl. Mostly because makeup and clothing are some of the coolest things on the planet and it's more socially acceptable for girls to enjoy them (but let's not open up that can of worms right now). I'm unashamed to say that this is one of the biggest reasons that I love things such as Larping and Theatre. All the dressing up!!
Today I am going to a mages in space larp and I have excitedly done my hair differently. Its pretty simple but I like it looots :D I french platted it back (always a struggle because I am way better at inverse braids) and then created a braid bun and put the flower in the middle of it all. Uber cool and took me 3 minutes to do.
To complete with my outfit I have brought my dirty overalls in the hopes of being some snobby first ship engineer. Its kind of gross that they are still grubby with car grease but it certainly adds to the outfit.
Crucible Badges!
So special snowflakes and Darkest Past players better watch out because I have the following badges! Brace yourselves!
Eigenvectors and Eigenvalues - The Sliced Bread of Mathematics
Eigenvectors and Eigenvalues are simply a property of any matrix which some clever cookie discovered were very useful in real life applications. You may not know them yet but these bad boys have improved your life. They were used to design the suspension springs on your car, they could have been used to design the foundations of the building you are sitting in, they even helped you out that one time on Facebook where you posted some photos and Facebook correctly guessed which of your friends were in the picture. And best of all, they're pretty simple to calculate. I'm introducing them now for your benefit because I will probably be talking about them later on. I'll explain them then I encourage you to give my example a try!
The Matrix (the real deal not the movie)
For those of you who aren't familiar with matrices (the rest of you can skip to the next paragraph) they are basically just a part of a set of linear equations. In this case because there are two rows, there are two equations which might be -5a + 2b = 4 and 2a -2b = 5. Don't panic! All I've done is taken the first half of both the equations, stacked them on top of each other and then factorized out the a's and b's. (I'll show you visual learners that in a picture). Also from now on (because its easier I will be representing matrices using the following notation [-5, 2; 2, -2] because its easier. ; indicates that the following numbers are on a lower row and , indicates that the following number is on a different column)
Eigenvalues
Alrightie, the first thing you have to do is recognize that the definition of an eigenvalue is det( I lambda - A) = 0 where lambda is a vector of your eigenvalues. I know that seems super duper weird and complex but I'll break it down for you."det" stands for the determinant of a matrix. Its just another useful property so don't freak out! A 2x2 matrix e.g [1, 2; 3, 4] can be found by multiplying the top right and bottom left elements of the matrix and then subtracting the top right element timed by the bottom left element. So for the example matrix I gave above this would be 1x4 - (2x3) = -2! Simple right. Good old primary multiplication and subtraction :)
"I" stands for an Identity matrix. This is one of the simplest matrices you will come across. Its just a matrix filled with zeros with 1's going down on a negative diagonal (\). for example a 2x2 identity matrix looks like this [1,0; 0,1].
"lambda" is just the two eigenvalues you want to find. Lambda is the name of a fancy Greek symbol but blogger doesn't know how to speak Greek so I can't write it in text but I can give you this link to good old wiki which has a picture of it http://en.wikipedia.org/wiki/Lambda
Lastly A is just the matrix that you are trying to find eigenvalues and eigenvectors for. Which in this case is our old friend [-5, 2; 2, -2].
So putting this together we have the following working...
Eigenvectors
Cool, cool cool cool. Now we have our eigenvalues we can use them to get the corresponding eigenvectors. Let's start with our eigenvalue -6.- The formula to get your eigenvectors is AX = lambdaX. Once again A is your matrix, lambda is a single eigenvalue. X represents your eigenvector that you are going to work out which for a 2x2 matrix looks like [x1 ; x2].
- We expand out our equation to get 2 linear equations (can be seen in the working below this massive chunk of text).
Now I know what you're thinking, by now you will already have tried to solve the two equations for x1 and x2 with no success right :P ?? If you have 2 unknowns and 2 equations you can solve something right?? WRONG! well, its right but in this case it doesn't apply. This is because of the way you worked out your eigenvalues using the A matrix. These two equations are actually the same equation with a couple of things thrown in. So if you try to solve it, the answer will always be zero. You need 2 distinct equations to solve something with 2 unknowns. But never fear the next step will explain all. - Eigenvectors are special because they don't just have one solution. They are able to have any solution so long as the ratio of X1:X2 remains the same. All we have to do is guess a value for X1 or X2 and using only one equation, work out the other X with respect to that value. To make things easy I am going to guess that X1 =1.
Give the other eigenvector a go using lambda = -1. See if you can get some scaled version of [1;2] :) YOU CAN DO IT!
Test Yourself!
Try this matrix out for size [0, 1; -2, -3]. See if you can get to the eigenvalues -1 and -2. Then see if you can get some scaled version of the eigenvectors [1,-1] and [1,-2]. If you do it I will give you a hi five next time I see you.Diagonalisation Time
So like many concepts in math, diagonalisation has a really complex looking definition. Luckily some smart cookies have come along and said "Hey, do you know what would make this a lot easier? Just *insert brilliant world changing idea here*".
A matrix A can be diagonalisable if you can find a matrix which is able to be used to transform your matrix into a matrix of the same size where the only non zero values are the ones on the diagonal *takes deep breath*. Mathematically this looks like this:
Luckily there are a number of very clever people who have figured out that...
- If the matrix A (having dimensions nxn) is diagonalisable, then there are n linearly independent eigenvectors of matrix A.
In other words if you have a 2x2 matrix, if you can prove that there are 2 linearly independent eigenvectors then you have proved that the matrix is diagonalisable.
This is AMAZINGLY AWESOME!! because we already know how to figure out both eigenvectors and whether two vectors are linearly independent. here is a link to my previous blog where I talk about linear independence
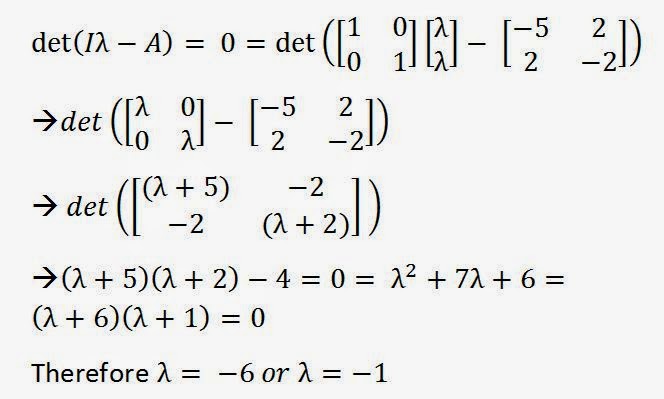
No comments:
Post a Comment